图例：

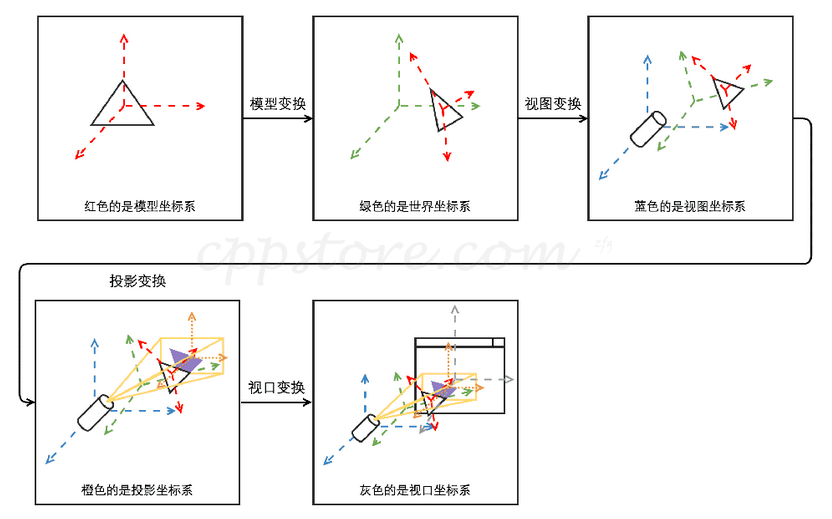
首先，在第一张图中的红色坐标系是模型坐标系，这意味着在这一步，程序员指定了模型的各个点的位置。每个点是 (x, y, z) 组成的数组，比如用 WebGL 的话，相关代码可能是类似这样的：

var vertices = [

1, 0, 0.5,

-0.5, 0, 0.5,

0, 1, 0

];

gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertices), gl.STATIC_DRAW);

后面的所有坐标变换都是 4x4 的齐次矩阵，所以这里除了每个点的 (x, y, z) 坐标之外，另外补上 1 组成 (x, y, z, 1) 的坐标。之所以使用齐次坐标，是为了将平移操作也统一成矩阵乘法的形式，如果用三维的坐标，就只能用两个矩阵向量相加表示，这样和旋转缩放就不统一了。

通过模型变换，把模型坐标转成世界坐标，就是第二张图中黑色的三角形相对于绿色的坐标系的坐标。世界坐标系就是所有模型共享的参考系，而模型坐标系是只对每个模型本身有意义的。为什么这么麻烦，不能直接在上一步写三个点的位置的时候，写成在绿色世界坐标系下的位置呢？想象一下，一个正三角形绕X 轴转 90°，再绕 Y 轴转30°，你能马上脑补出它旋转后每个点的坐标吗？即使可以，在更加复杂的场景下，这都会是一件非常困难的事。所以，模型变换解决的是，把物体在世界坐标系下的位置拆分成旋转、平移、缩放的表达方式。

视图变换的作用就更难理解了吧？它可以理解为，指定一个照相机的位置和角度，然后去观察世界坐标系下的物体。为什么不能把照相机的位置定在世界坐标系原点，看向Z方向负方向？当然也不是不能这样，只是很多时候做动画效果，场景中的物体可能是不变的，变的只是观察的位置和方向。这样的话，如果脑补观察位置改变后，模型所在的世界坐标，就像上面说的脑补在世界坐标系下的位置一样不直观。另外，既然世界上那么多模型是不动的，那么之前的其他矩阵的乘积也能被存下来复用，只要做一次乘以视图变换矩阵的操作，而非上图中的四次变换矩阵，减少矩阵乘法操作使得算法效率更高。

模型变换和视图变换都是通过旋转、平移、缩放的矩阵相乘实现的，具体矩阵参见：World, View and Projection Transformation Matrices。其实这里都是各种参考系的概念，就像我们在物理课上学到的相对的概念，坐在开动的车上的人会觉得是外部的世界在倒退，我们很容易想到，把照相机往一个方向上移动，相当于把观察对象往另外一个方向上移动。所以就有了模型视图矩阵的概念，本质上就是模型变换矩阵和视图矩阵相乘，但是如果把这个相乘结果存起来，对模型的点做批处理的话，效率就会比每个点去乘两次矩阵高得多。

投影变换就比较有意思了，它是把前面在三维空间中的坐标投影到二维屏幕坐标，但是计算结果也是一个三维坐标（严格来说是四维的，还有个齐次的 1），除了屏幕的横纵坐标之外，另一个维度就是垂直屏幕方向上的深度坐标，就是之后可以写入深度缓冲器的值。至于如何将三维坐标转换到二维屏幕，主要分为正交投影和透视投影，都是用相似三角形算比例，不同在于前者的实景体是一个长方体，而后者是一个梯台。需要注意的是，照相机的位置和旋转等值是在视图变换中就已经指定的，而投影变换只是三维到二维的过程。在第四张图中表现为紫色的三角形在橙色的坐标系下的位置。这里有非常好的通过相似三角形计算投影后的位置的文章，建议有兴趣的看一下。

最后就是视口变换了，到这一步其实已经很简单了！相比前面又是旋转平移缩放，又是相似三角形计算的，这里只是一个非常简单的 XoY平面上的缩放，它决定了最终渲染到平面的哪一块，所以用之前的缩放同样处理就能得到相应矩阵了。甚至你都不用写矩阵，即使在 WebGL里，也有直接设定视口（View Port）的命令。

gl.viewport(0, 0, this._canvas.width, this._canvas.height);

终于要大功告成了！接下来就是把这些矩阵拼起来了！（终于到了我能说“矩阵乘一乘啊”的时候了！）

变换后的坐标 = 视口矩阵 x 投影矩阵 x 视图矩阵 x 模型矩阵 x 模型点坐标

这里除了模型点坐标和变换后的坐标是 1x4 的向量之外，其他矩阵都是 4x4 的。虽然按理说是从右边到左边计算的，但很多时候左边的几个矩阵都是不变的，这时候可以把这些矩阵缓存起来，下次就直接成结果的一个矩阵就好。

投影矩阵的计算方法

电脑显示器是2D表面。由OpenGL渲染的3D场景必须作为2D图像投影到计算机屏幕上。GL_PROJECTION矩阵用于此投影变换。首先，它将所有顶点数据从眼睛坐标转换为剪辑坐标。然后，这些片段坐标还通过除以片段坐标的w分量而转换为归一化设备坐标（NDC）。

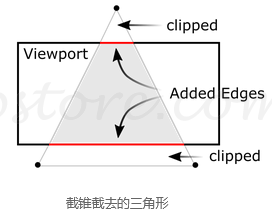
因此，我们必须记住，裁剪（视锥剔除）和NDC转换都已集成到GL_PROJECTION 矩阵中。以下各节描述了如何从6个参数构建投影矩阵。left，right，bottom，top，近边界和远边界值。

请注意，正好在用w c划分之前，在剪辑坐标中执行了平截头体剔除（裁剪）。夹子坐标x Ç，Y Ç和z Ç通过用瓦特比较测试Ç。如果任何剪辑坐标小于-w c或大于w c，则顶点将被丢弃。

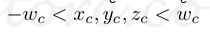
然后，OpenGL将在发生剪裁的位置重建多边形的边缘。

透视投影

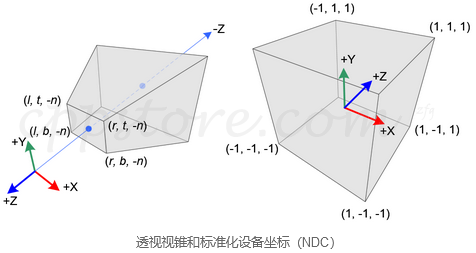
在透视投影中，将截锥形的视锥中的3D点（眼睛坐标）映射到立方体（NDC）。x坐标从[l，r]到[-1，1]的范围，y坐标从[b，t]到[-1，1]的范围，z坐标从[-n，-f]的范围到[-1，1]。

注意，眼睛坐标是在右手坐标系中定义的，但是NDC使用左手坐标系。也就是说，原点的相机在眼空间中沿-Z轴方向观看，但在NDC中沿+ Z轴方向观看。由于glFrustum（）接受的唯一的正值附近及远的距离，我们需要GL_PROJECTION矩阵的施工过程中否定他们。

在OpenGL中，眼睛空间中的3D点投影到近平面（投影平面）上。下图显示了眼空间中的点（x_e，y_e，z_e）如何投影到近平面上的（x_p，y_p，z_p）。

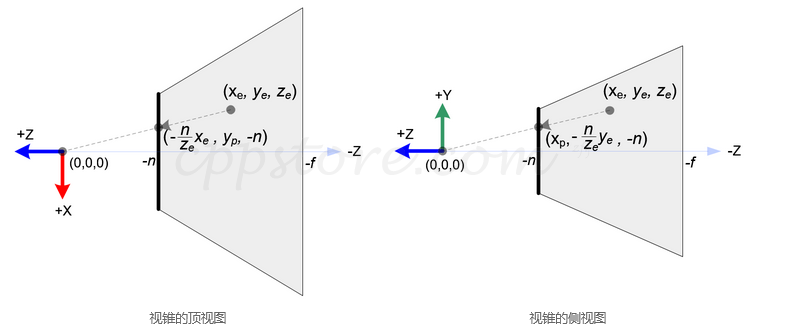
从视锥的顶视图来看，眼空间的x坐标x_e映射到x_p，而x_p是通过使用相似三角形的比率来计算的；

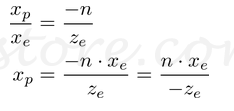
从视锥的侧面看，y_p的计算方法也与此类似。

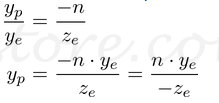
注意，x_p和y_p都取决于z_e；它们与-z e成反比。换句话说，它们都被-z_e除。这是构造GL_PROJECTION矩阵的第一个线索。在通过乘以GL_PROJECTION矩阵对眼睛坐标进行变换之后，剪辑坐标仍然是齐次坐标。通过除以剪辑坐标的w分量，最终成为归一化的设备坐标（NDC）。（请参阅有关OpenGL转换的更多详细信息。）

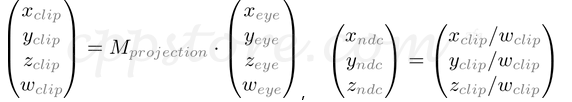
因此，我们可以将剪辑坐标的w分量设置为-z_e。并且，GL_PROJECTION矩阵的第4个变为（0，0，-1，0）。

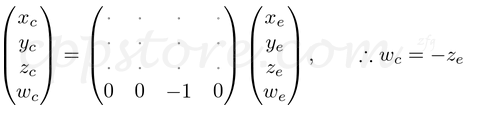
接下来，我们以线性关系将x_p和y_p映射到NDC的x_n和y_n。[l，r]⇒[-1，1]和[b，t]⇒[-1，1]。

然后，将x_p和y_p代入上述方程式。

请注意，我们将每个方程式的两个项都用-z_e除以进行透视划分（x_c / w_c，y_c / w_c）。并且我们将w_c设置为-z_e较早，并且括号内的项变为clip coordiantes的x_c和y_c。

从这些方程式中，我们可以找到GL_PROJECTION矩阵的第一行和第二行。

现在，我们只需要解决GL_PROJECTION矩阵的第三行。找到z_n与其他位置略有不同，因为在眼睛空间中的z_e总是在近平面上投影为-n。但是我们需要唯一的z值进行裁剪和深度测试。另外，我们应该能够取消投影（逆变换）。由于我们知道z不依赖于x或y值，因此我们借用w分量来查找z_n与z_e之间的关系。因此，我们可以像这样指定GL_PROJECTION矩阵的第三行。

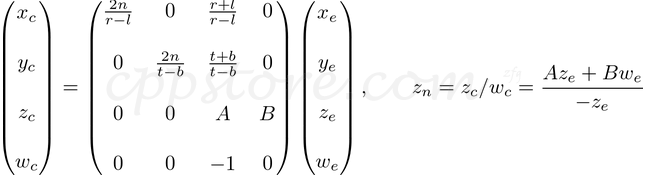
在眼空间中，w e等于1。

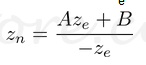
为了找到系数A和B，我们使用（z_e，z_n）关系；（-n，-1）和（-f，1），并将它们放入上式中。

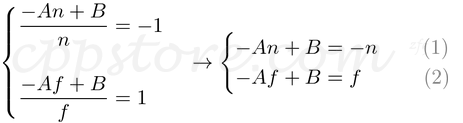
为了求解A和B的方程，对B重写等式（1）；

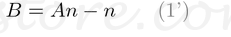
将等式（1'）替换为等式（2）中的B，然后求解A；

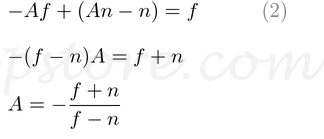
将A放入等式（1）中找到B ;

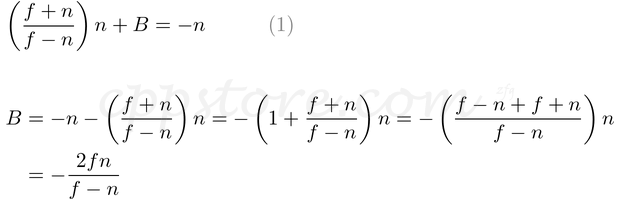
我们发现一个和乙。因此，z_e和z_n之间的关系变为：

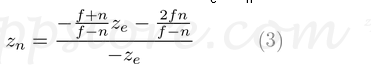
最后，我们找到了GL_PROJECTION矩阵的所有条目。完整的投影矩阵为：

该投影矩阵用于一般的平截头体。如果观看量是对称的，即和，则可以简化为；

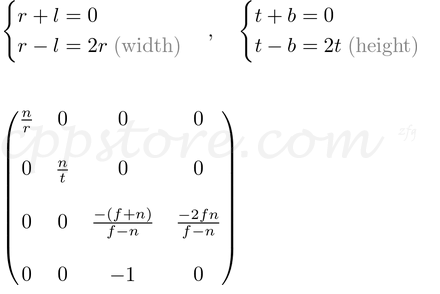
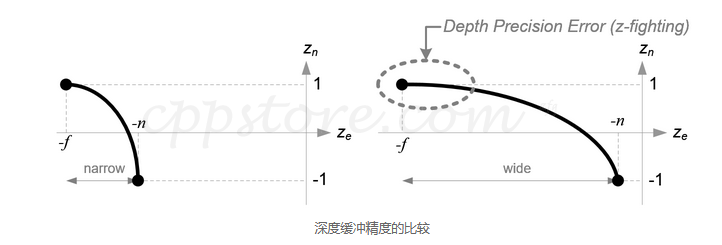
在继续之前，请再次看一下z_e和z_n之间的关系，式（3）。您会注意到它是有理函数，并且是z_e和z_n之间的非线性关系。这意味着在近平面上有非常高的精度，而在远平面上有非常低的精度。如果范围[-n，-f]变大，则会引起深度精度问题（z战斗）。z_e在远平面附近的小变化不会影响z_n值。n和f之间的距离应尽可能短，以最大程度地减少深度缓冲区的精度问题。

发布时间: 4年前【前端开发】112人已围观【返回】【回到顶端】

转载：个人转载请注明文章出处 "www.itarticle.cc-IT技术类文章收集&分享"。

很赞哦！ (3)