客户端导出navmesh数据操作

1. 将地图取名为map101，创建行走层对象xingzouceng，添加Mesh Renderer，Mesh Filter，Mesh Collider组件
2. 烘培行走层对象
3. 点击测试地图大小，修改地图范围
4. 点击生成巡逻数据
5. 操作窗口 客户端地图
6. 服务器寻路操作

在unity客户端工程中将生成的101.navmesh数据复制到工程目录中，运行服务器检测客户端 服务器寻路

寻路方式

多边形寻路

多边形寻路参考PolygonNavMesh 原理：

1. 将unity导出的数据生成凸多边形
2. 找出所有凸多边形共享的边
3. 使用A*算法找出起点到目标点所经过的多边形列表
4. 使用漏斗算法找出顶点坐标

unity寻路网格导出脚本PolygonNavMeshWindow

三角形寻路

三角形寻路参考TriangleNavMesh 原理同多边形

顶点寻路

顶点寻路参考NodeNavMesh 直接A*搜索顶点坐标

总结

多边形寻路和三角形寻路由于原理相同，性能消耗差不多，由于多边形合并了三角形，速度稍微快一些；顶点寻路相比于多边形寻路慢了5~40倍

多边形寻路需要导出的寻路数据在行走层中没有额外的顶点，共边顶点坐标需要一致，顶点寻路由于由于采用阻挡区三角形顶点寻路，因此没有此限制，但是增加了额外的阻挡区数据

多边形寻路支持3D寻路，顶点寻路只能平面寻路

图解NavMesh寻路中的漏斗算法

NavMesh是广泛使用的一种寻路技术，将地图中可走的部分生成连续的多边形/三角形网格，寻路在网格中进行，主要包含两步：

1、根据网格的邻接信息构造图，使用A*之类的寻路算法计算出从起点到重点需要走过的多边形/三角形集合；

2、使用漏斗算法/拉绳子算法，将多边形列表转换为一条最优的路店。本文主要讲一下对于三角形列表的漏斗算法原理。

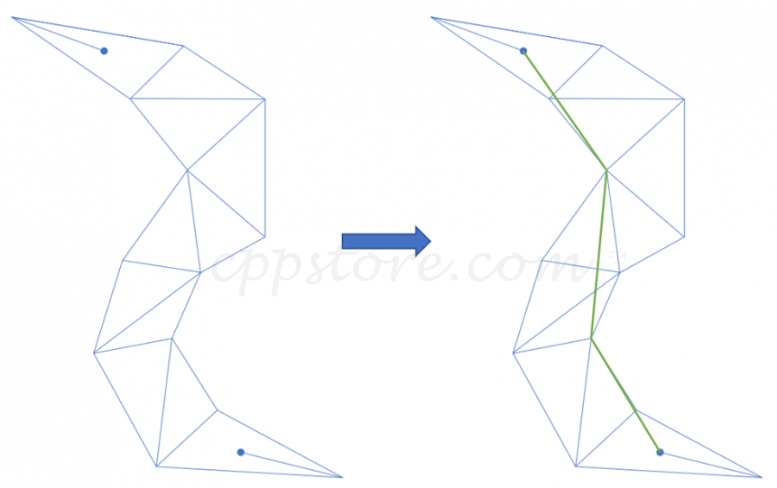
算法结果

如图所示，假定左边的三角形列表是从寻路算法生成的从起点到终点需要经过的三角形，两个蓝色圆点分别是起点和重点；右边绿色的粗线就是算法的结果，是从起点到终点需要经过的最短路径。

算法过程

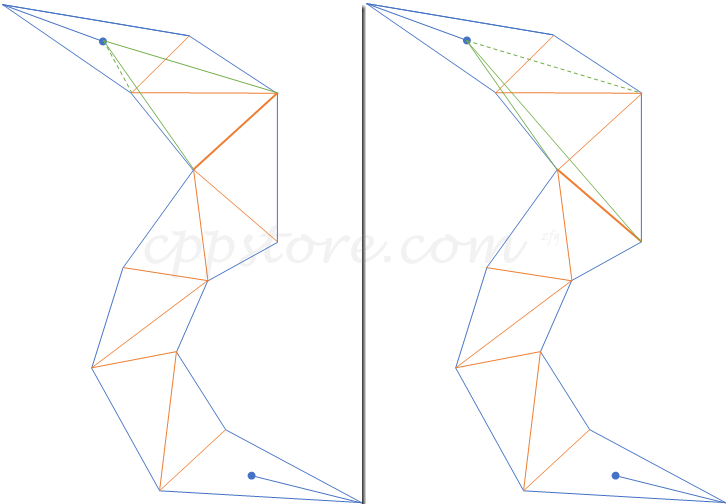
1.首先计算出三角形列表中的邻接边列表，所谓邻接边就是两个三角形公用的边，然后从起点开始，构造到第一条邻接边的漏斗，算法正式开始。黄色的边均为邻接边，两条绿色的边为初始的漏斗，姑且约定两条“漏斗边”的“起点”为蓝色圆点，方便后文的描述

2.

将两条漏斗边的终点移动到下一条邻接边，对于途中的情况，左边的边没有动（但逻辑上算移动了），右边的边向内收紧了。分别考虑两条边的角度变化，当漏斗变窄（或不变化）时，本次移动是有效的，否则需要对那条边回退操作，对于图中情况，移动是有效的

可见图中的漏斗变窄了

3.继续将漏斗边的终点移动到下一条邻接边，漏斗继续收紧，移动有效，之后的两步操作都和上图情况相同

4.下一步操作出现了第一种特殊情况，漏斗边终点移动到下一条邻接边时，漏斗口的角度变为了负数（原来右边漏斗边转到了左边去），这种情况下，被盖过去的那条边的终点就成为了结果中的第一个点。同时，将漏斗起点移动到该点，以当前漏斗起点所在三角形的出邻接边构造漏斗，继续算法

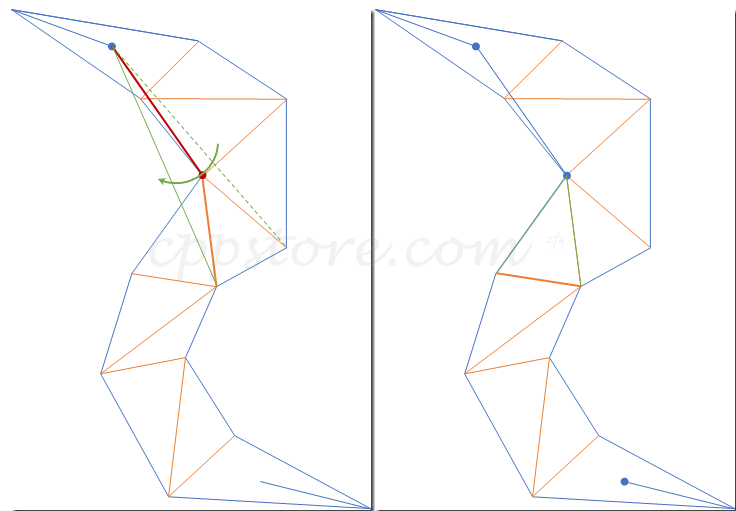
5.使用之前描述的规则继续收紧漏斗口

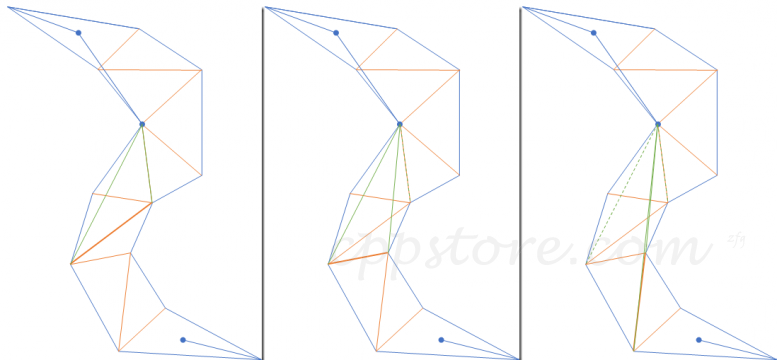
6.继续移动漏斗，这一次会发现左边的漏斗边没有移动，而右边的漏斗边会使漏斗口变大，右边的移动是无效的。这次移动只有左边发生了移动（虽然起点和终点一样）

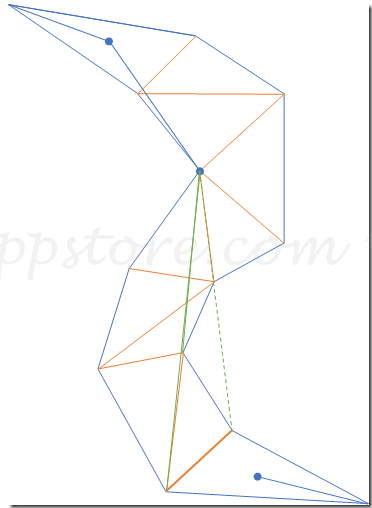
7.下面是算法的结束情况，算法已经移动到了最后一条邻接边，但是从现在的漏斗底直接连一条线到终点肯定是不可行的。随后我们以终点一个点，当作一条两条端点相同的边。用它继续前进漏斗口。右边的漏斗边如果移动，会使漏斗口变大，因此不移动，左边的漏斗边移动，会盖过右边的漏斗边，因此右边的漏斗边终点成为了结果中的另一个点。

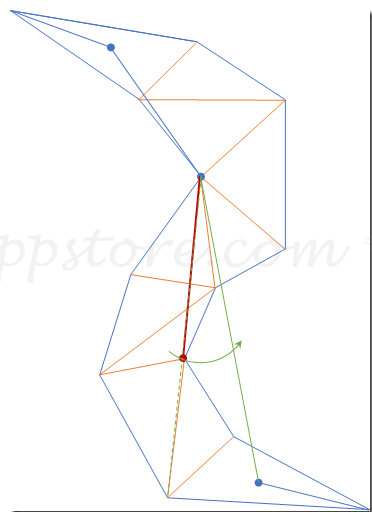
8.同样，以该点所在三角形的出邻接边重新构造漏斗，继续算法，很快就会发现漏斗口到终点，收到了最小，算法结束。

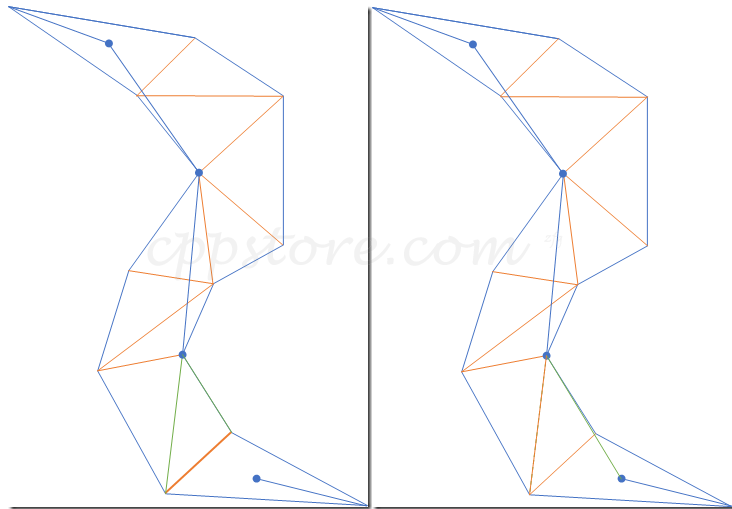
3d 游戏的寻路算法主要还是A* （a-star，A星）使用的比较广泛，它有快速、路径短，不成环等优点，在orge，unity等引擎中得到了广泛的使用。

A*的最初设计是基于2d平面，对于3d 寻路就需要先对场景网格化，生成平面，把3d的问题转化为2d的问题，然后就可以通过A*进行寻路。

3d 游戏寻路大致分为2部分：navmesh(3d转2d)、A*算法

网格数据（navmesh）生成：

1、Voxelization – Create a solid heightfield from the source geometry.

2、Generate Regions – Detect the top surface area of the solid heightfield and divide it up into regions of contiguous spans.

3、Generate Contours – Detect the contours of the regions and form them into simple polygons.

4、Generate Polygon Mesh – Sub-divide the contours into convex polygons.

5、Generate Detailed Mesh – Triangulate the polygon mesh and add height detail.

相关概念： 体素化Voxelization 向量空间(vector space) 到 体素空间(voxel space) 的转换. 用到的是叫保守体素化(Conservative voxelization) 的算法, 它保证了每个多边形面都能完全被生成的三维象素(voxel)包裹。

体素化后, 生成的都是可寻路的高度场(heightfield)信息, 不可寻路部分被剔除.这一步是从一个固态高度场(solid heightfield) 生成一个开放高度场(open heightfield) 的过程, 一个开放高度场表示在一个固态空间上可能寻路的平面.

区域生成Region Generation 定义,哪部分的面是可以寻路的, 并且把寻路区域分隔成连续的平面以供最后生成简单寻路多边形. 最终结果, 墙体,围栏, 柱子, 桌子底等不可能寻路的平面在这步根据邻居信息和分水岭算法(the watershed algorithm) 被剔除, 一些孤立的小局域(比如桌子表面) 也被剔除. 楼梯, 虽然是多级, 也会被当做一个平面(绿色). 楼梯扶手等平面也被剔除.

轮廓生成Contour Generation 完成从体素空间回到向量空间的转换. 区域(region) 轮廓将被"遍历(walk)", 形成简单的多边形.其中, 有些区域被合并, 多边形的边更平滑, 边长度被优化. 此时，可寻路区域已经被一些简化的多边形所表示。

凸多边形生成Convex Polygon Generation：把多边形切分为三角形, 而后尽量合并的方式 精细网格生成

Detailed Mesh Generation： 通过"德劳内三角化"(Delaunay triangulation) 算法三角化成包含高度信息的三角形，顶点信息也会在这里补到各个三角形上, 以保证高度信息和模型保持一致.

A* （a-star，A星）大致描述：

1、把起始格添加到开启列表。

2、寻找开启列表中F值最低的格子(当前格)，将其切到关闭列表

3、对相邻的8格最如下处理：如果它不在开启列表中，把它加进去 ；如果它已经在开启列表中，用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。如果这样，把这一格的父节点改成当前格，并且重新计算这一格的G和F值。如果你保持你的 开启列表按F值排序，改变之后你可能需要重新对开启列表排序。

4、当把目标格添加进了关闭列表，这时候路径被找到；如果没有找到目标格，开启列表已经空了，这时候，路径不存在。 最后，保存路径，从目标格开始，沿着每一格的父节点移动直到回到起始格。这就是需要的路径。

(1-4是个循环过程)

附注：

开启/关闭列表：临时记录区，算法中的变量

G值：从起点A，沿着产生的路径，移动到网格上指定方格的移动耗费。

H值：从网格上那个方格移动到终点B的预估移动耗费。

F值：G + H 父节点：记录最短路径

A*（A-Star)算法：公式： f(n)=g(n)+h(n)

f(n) 是节点n从初始点到目标点的估价函数

g(n) 是在状态空间中从初始节点到n节点的实际代价

h(n)是从n到目标节点最佳路径的估计代价 最短路径，关键在于估价函数h(n)： 估价值h(n)<= n到目标节点的距离实际值，搜索的点数多，搜索范围大，效率低。但能得到最优解。

估价值>实际值, 搜索的点数少，搜索范围小，效率高，但不能保证得到最优解。 估价值与实际值越接近，估价函数取得就越好 对几何路网来说，取两节点间欧几理德距离（直线距离）做为估价值，即f=g(n)+sqrt((dx-nx)*(dx-nx)+(dy- ny)*(dy-ny))；这样估价函数f在g值一定的情况下，会或多或少的受估价值h的制约，节点距目标点近，h值小，f值相对就小，能保证最短路的搜索向终点的方向进行。

算法的搜索过程： 创建两个表，OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。 遍历当前节点的各个节点，将n节点放入CLOSE中，取n节点的子节点X,->算X的估价值。

伪代码： While(OPEN!=NULL)

{

从OPEN表中取估价值f最小的节点n;

if(n节点==目标节点)

break;

else

{

if(X in OPEN) 比较两个X的估价值f //注意是同一个节点的两个不同路径的估价值 if( X的估价值小于OPEN表的估价值 ) 更新OPEN表中的估价值; //取最小路径的估价值

if(X in CLOSE) 比较两个X的估价值 //注意是同一个节点的两个不同路径的估价值 if( X的估价值小于CLOSE表的估价值 ) 更新CLOSE表中的估价值; 把X节点放入OPEN //取最小路径的估价值

if(X not in both) 求X的估价值; 并将X插入OPEN表中; //还没有排序 } 将n节点插入CLOSE表中; 按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小，从最小路径的节点向下进行。

}

关于寻路：可以用开源的 RecastNavigation ，里面就有上述算法的实现和demo，支持unity 3d的寻路。

可以用来做地图服务器的案例。 https://github.com/memononen/recastnavigation

unity 3d导航数据的导出要将任意的 Mesh 转换成 rcPolyMes，生成相应的多边形和邻边；这里每个多边形设置为基础的三角形， 然后用内建的函数来优化合并多边形，接着再建立邻边即可，这样就可以得出最优化的 NavMesh 最终数据。

注意：Unity 在导出 NavMesh的数据是包含 NavMesh 中得多边形 Poly信息，可以利用这个直接建立多边形，这样下来数据最接近unity本身的数据。

发布时间: 5年前【游戏相关】130人已围观【返回】【回到顶端】

转载：个人转载请注明文章出处 "www.itarticle.cc-IT技术类文章收集&分享"。

很赞哦！ (1)